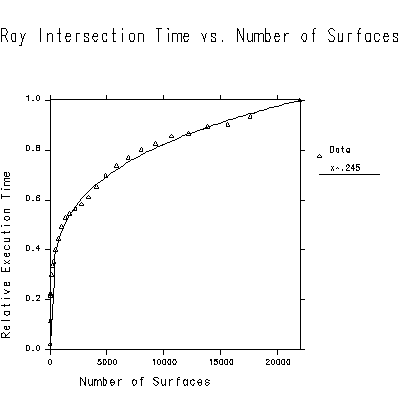
Figure 10. Plot showing sublinear relationship of intersection time to number of surfaces in a scene. The best fit for the exponent in this test was 0.245, meaning the ray intersection time grew more slowly than the fourth root of N. The spheres were kept small enough so that a random ray sent from the field's interior had about a 50% chance of hitting something. (I.e. the sphere radii were proportional to N^1/3.) This guarantees that we are really seeing the cost of complicated geometry, since each ray goes by many surfaces.Although it is difficult to prove in general, our empirical tests show that the average cost of ray intersection using this technique grows as a fractional power of the total number of surfaces, i.e. O(N ^ gamma ) where gamma < 0.5. The time to create the octree grows linearly with the number of surfaces, but it is usually only a tiny fraction of the time spent rendering. Figure 10 shows the relationship between ray intersection time and number of surfaces for a uniformly distributed random field of spheres.
The basic surface primitives supported in Radiance are polygons, spheres and cones. Generator programs provide conversion from arbitrary shape definitions (e.g. surfaces of revolution, prisms, height fields, parametric patches) to these basic types. Additional scene complexity is modeled using hierarchical instancing, similar to the method proposed by Snyder [21]. In our application of instancing, objects to be instanced are stored in a separate octree, then this octree is instanced along with other surfaces to create a second, enclosing octree. This process is repeated as many times and in as many layers as desired to produce the combined scene. It is possible to model scenes with a virtually unlimited number of surfaces using this method.
Figure 11 shows a cabin in a forest. We began with a simple spray of 150 needles, which were put into an octree and instanced many times and combined with twigs to form a branch, which was in turn instanced and combined with larger branches and a trunk to form a pine tree. This pine tree was then put in another octree and instanced in different sizes and orientations to make a small stand of trees, which was combined with a terrain and cabin model to make this scene. Thus, four hierarchical octrees were used together to create this scene, which contains over a million surfaces in all. Despite its complexity, the scene still renders in a couple of hours, and the total data structure takes less than 10 Mbytes of RAM.