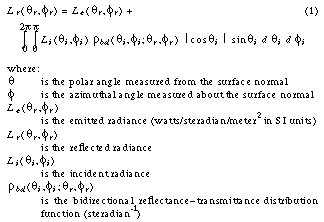
This equation is essentially Kajiya's rendering equation [10] with the notion of energy transfer between two points replaced by energy passing through a point in a specific direction (i.e. the definition of radiance). This formula has been documented many times, going back before the standard definition of the BRDF [16]. Its generality and simplicity provide the best foundation for building a lighting simulation.
This formulation of the rendering problem is a natural for ray tracing because it gives outgoing radiance in terms of incoming radiance over the projected sphere, without any explicit mention of the model geometry. The only thing to consider at any one time is the light interaction with a specific surface point, and how best to compute this integral from spawned ray values. Thus, no restrictions are placed on the number or shape of surfaces or surface elements, and discretization (meshing) of the scene is unnecessary and even irrelevant.
Although it is possible to approximate a solution to this equation using uniform stochastic sampling (i.e. Monte Carlo), the convergence under most conditions is so slow that such a solution is impractical. For example, a simple outdoor scene with a ground plane, a brick and the sun would take days to compute using naive Monte Carlo simply because the sun is so small (0.5\(de of arc) in comparison to the rest of the sky. It would take many thousands of samples per pixel to properly integrate light coming from such a concentrated source.
The key to fast convergence is in deciding what to sample by removing those parts of the integral we can compute deterministically and gauging the importance of the rest so as to maximize the payback from our ray calculations. In the case of the outdoor scene just described, we would want to consider the sun as an important contribution to be sampled separately, thus removing the biggest source of variance from our integral. Instead of relying on random samples over the hemisphere, we send a single sample ray towards the sun, and if it arrives unobstructed, we use a deterministic calculation of the total solar contribution based on the known size and luminosity of the sun as a whole. We are making the assumption that the sun is not partially occluded, but such an assumption would only be in error within the penumbra of a solar shadow region, and we know these regions to represent a very small portion of our scene.
Light sources cause peaks in the incident radiance distribution. Directional reflection and transmission cause peaks in the scattering function. This will occur for reflective materials near the mirror angle, and in the refracted direction of dielectric surfaces (e.g. glass). Removing such peak reflection and transmission angles by sending separate samples reduces the variance of our integral at a comparatively modest cost. This approach was introduced at the same time as ray-tracing by Whitted [31]. Further improvements were made by adding stochastic sampling to the deterministic source and specular calculations by Cook in the first real linking of stochastic and deterministic techniques [5]. Radiance employs a tightly coupled source and specular calculation, described in [29].