Our goal then is to design a filter that will spread the influence of q ``noise'' pixels into a larger region of Q pixels. We want to spread these pixels out without changing the total energy in the image, and without changing any pixel values unnecessarily.
First, to meet the goal of preserving energy, the filter must be applied to floating point sample values before the application of the tone operator. For example, take a simple tone operator that scales values by (128/.001), and clips values over 255. Consider a box filter in 1-D on the three values .0001, .001, and 1. If used before the tone operator, the filter gives 0.3337 and the pixel is clipped to a value of 255. If the tone operator is used first, the values become 13, 128 and 255, and the filter erroneously produces a result of 132.
Because we also want minimal disruption of pixels which are not in noisy areas, we want to design a filter that spreads the influence of ``noise'' pixels only. Because we are working from the point of view of constructing rather than analyzing an image, we construct our filter from a different point of view than usual.
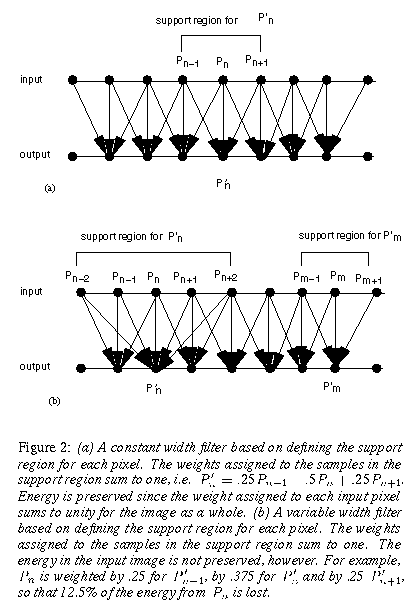
Figure 2 diagrams typical digital filters. A support region is defined for each output pixel. This region may be uniform, as shown in (a). This has the energy preserving property we seek, but has the disadvantages of blurring detail and not adequately distributing some values. A variable width region may be used to change the influence of some input samples [6]. However, as shown in the example in (b), this type of variable width kernel does not preserve all of the energy in the original sample set.
We propose constructing energy preserving filters based on the region of influence of each input sample, rather than defining a support region for each output sample. This is diagrammed in Fig. 3. A region is defined for each input sample. The weights assigned to the sample as it is distributed to the output image sum to one, and energy is preserved. By varying the region of influence for each input sample, large areas of the image can remain unaffected by the filter and the input image is disrupted a minimal amount.
The design of any input based energy preserving filter requires two rules: 1) a rule to identify ``noise'' inputs, and 2) a rule to determine the region into which the ``noise'' inputs will be distributed.